GAMES 101 学习笔记

仅作个人笔记记录

Lecture 03 Transformation

简单线性变换

\[ \begin{bmatrix} x^{\prime} \\ y^{\prime} \end{bmatrix}= \begin{bmatrix} s_x & 0 \\ 0 & s_y \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} \]\[ \begin{bmatrix} x^{\prime} \\ y^{\prime} \end{bmatrix}= \begin{bmatrix} 1 & a \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} \]\[ \mathbf{R}_\theta= \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} \]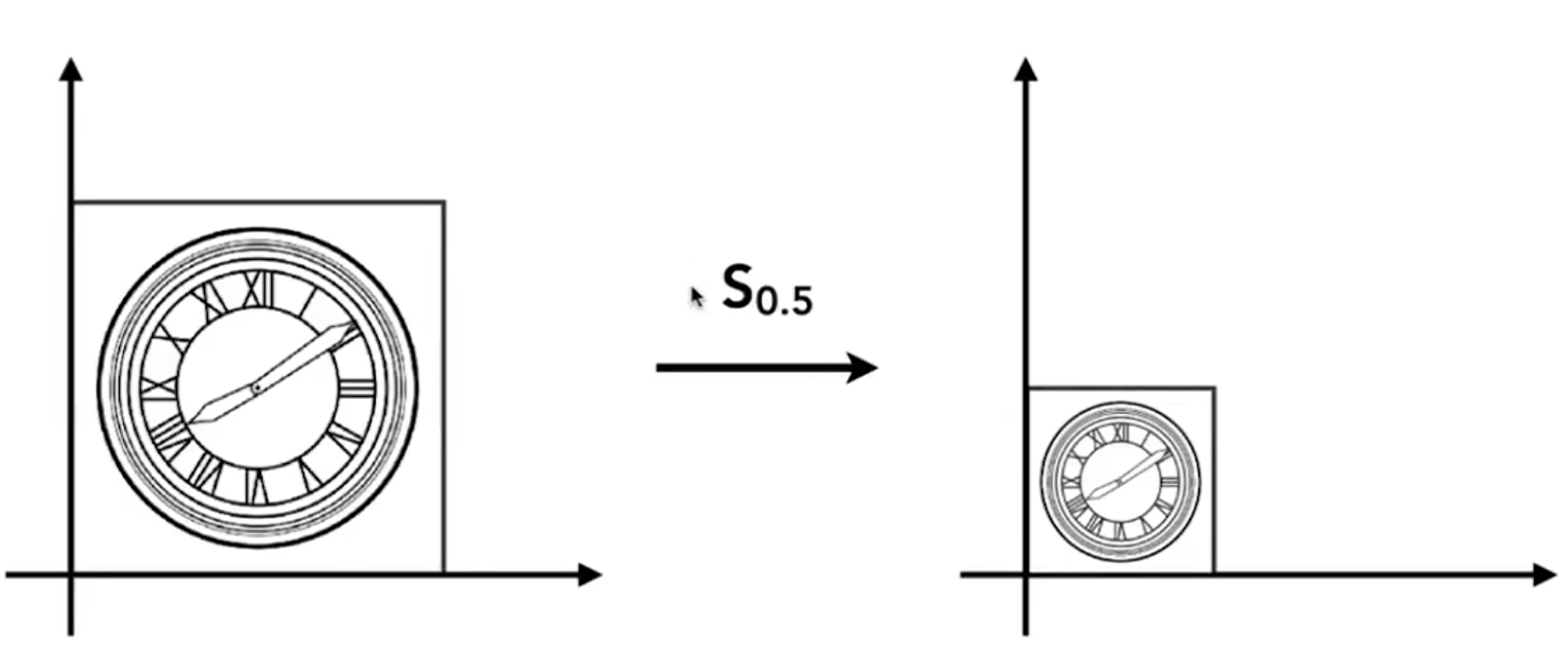

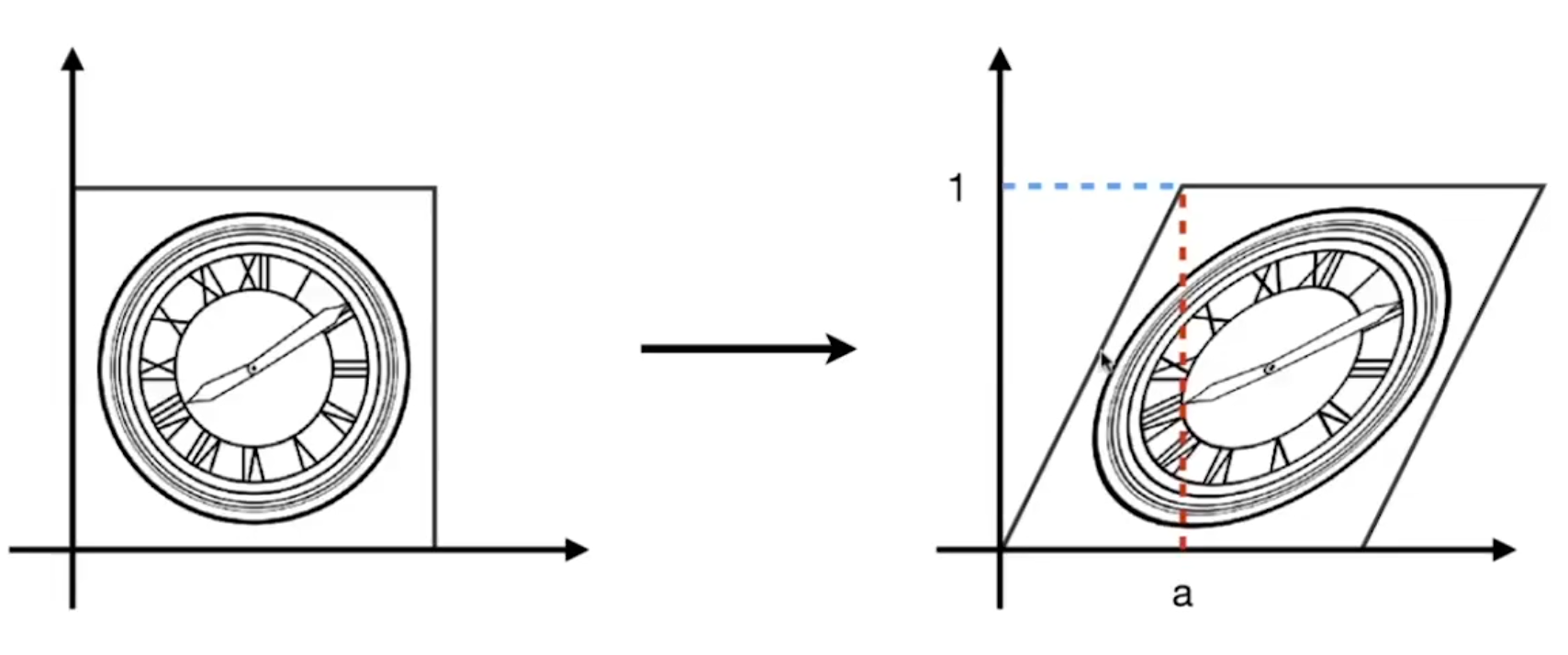
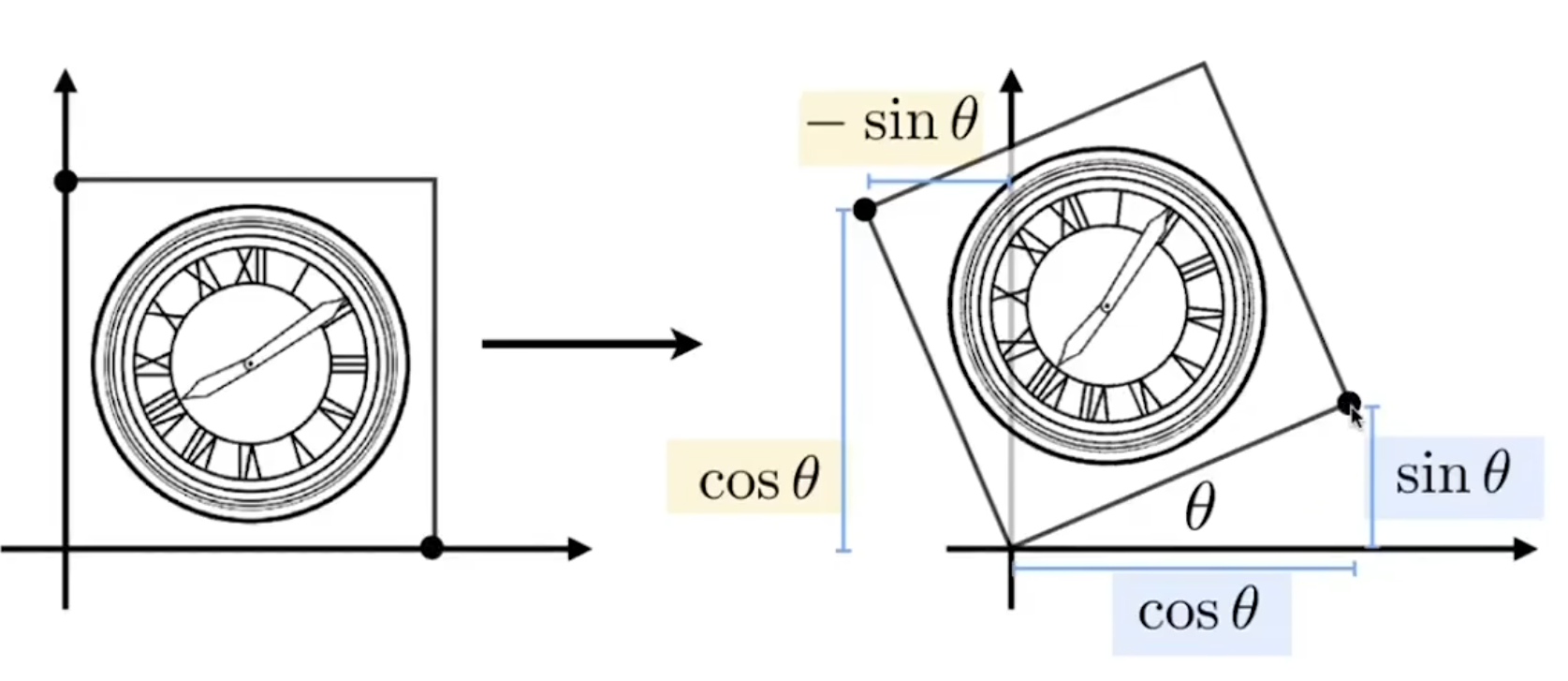
齐次坐标

重点：射影几何前置

你真的见过射影变换吗？【MaExpo】_哔哩哔哩_bilibili

【射影几何】从无穷远出发（一）_哔哩哔哩_bilibili

【射影几何】挪动数轴上的无穷远点（二）_哔哩哔哩_bilibili

【射影几何】二维坐标需要三个参数？齐次坐标的引入（四）_哔哩哔哩_bilibili

等距变换-->相似变换-->仿射变换-->射影变换

多视图几何笔记（二）射影变换-CSDN博客

\[ \begin{aligned} &s &缩放矩阵\\ &R &旋转矩阵\\ &t &平移矩阵\\ &K &仿射矩阵(非均匀缩放)\\ \end{aligned} \]

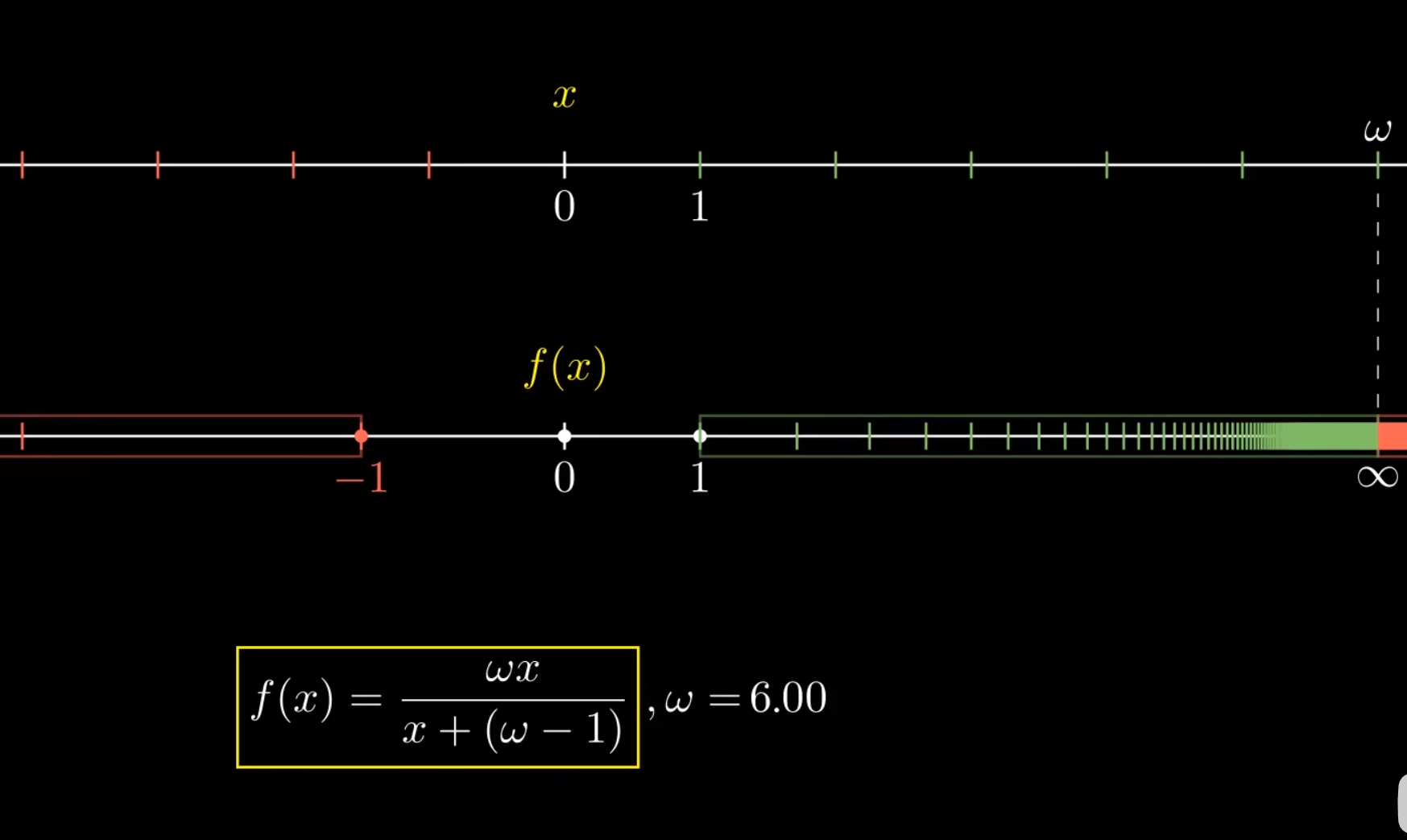
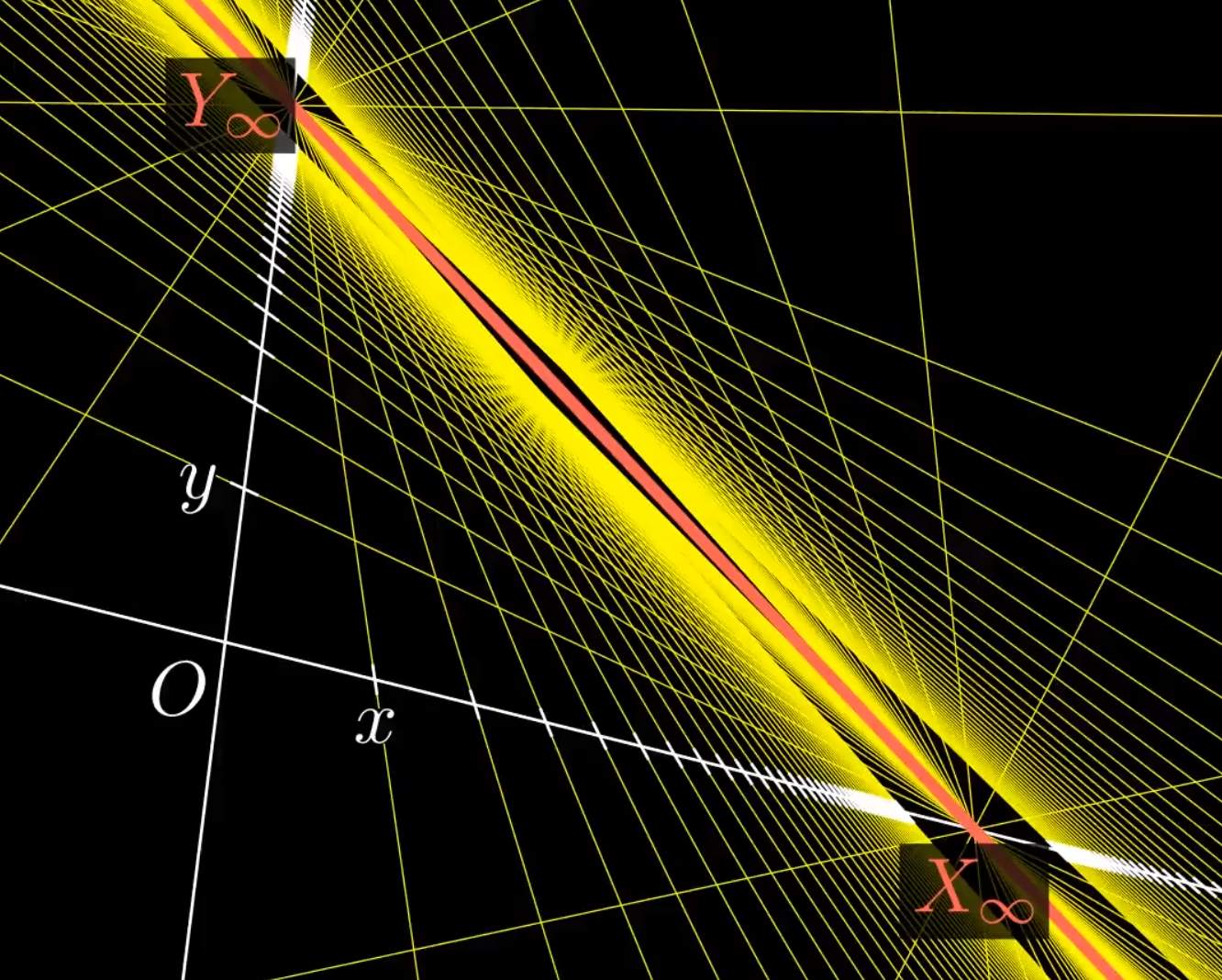
可以看出，对于仿射变换，理想点变换后还是理想点；对于射影变换，理想点被映射到有限点。说明射影变换能对消影点建模。

Lecture 04 Transformation Cont.

模型变换

把模型缩放、旋转、平移到世界坐标系某个位置

视图变化

就是把世界坐标系变换为屏幕空间坐标系，应用了正交矩阵的逆是转置的特性

投影

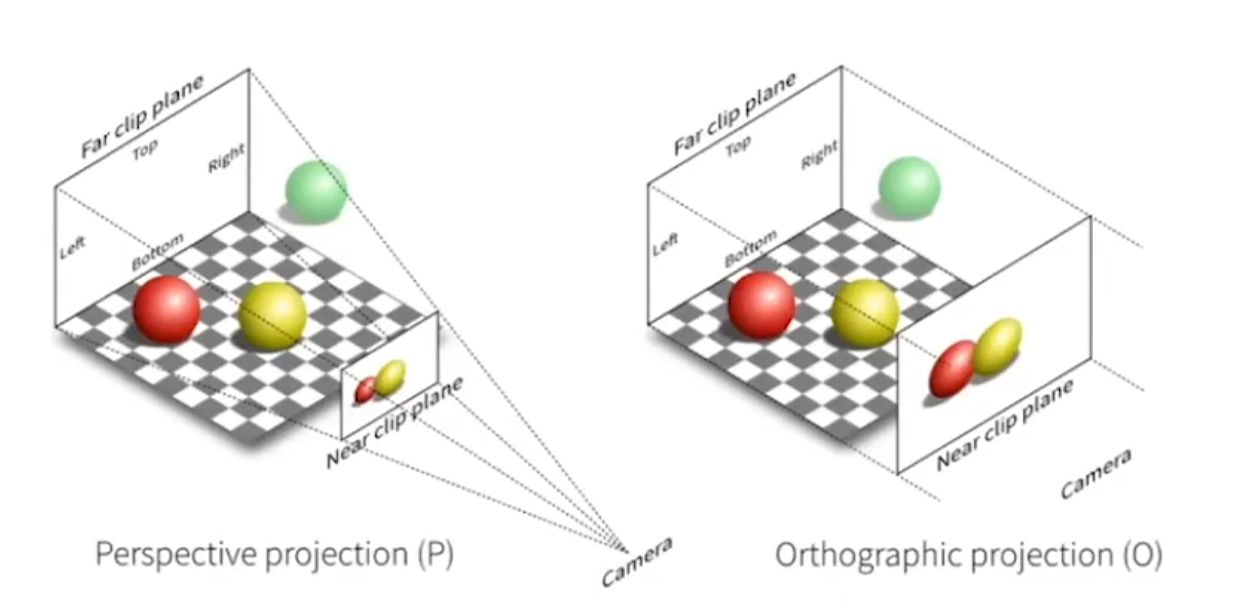
正交投影 vs 透视投影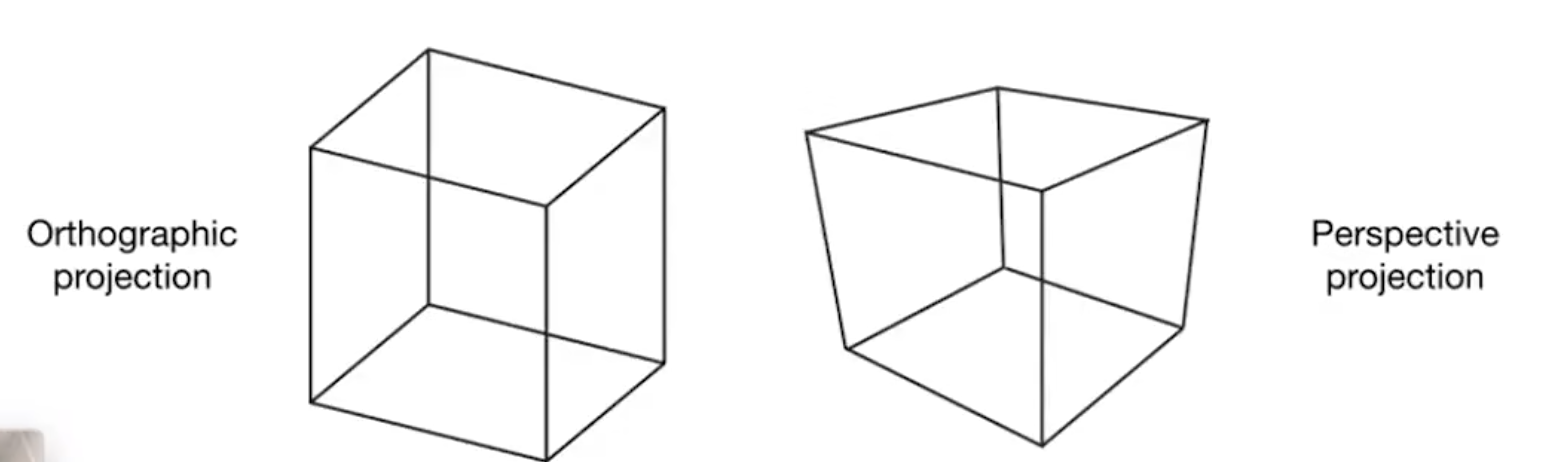

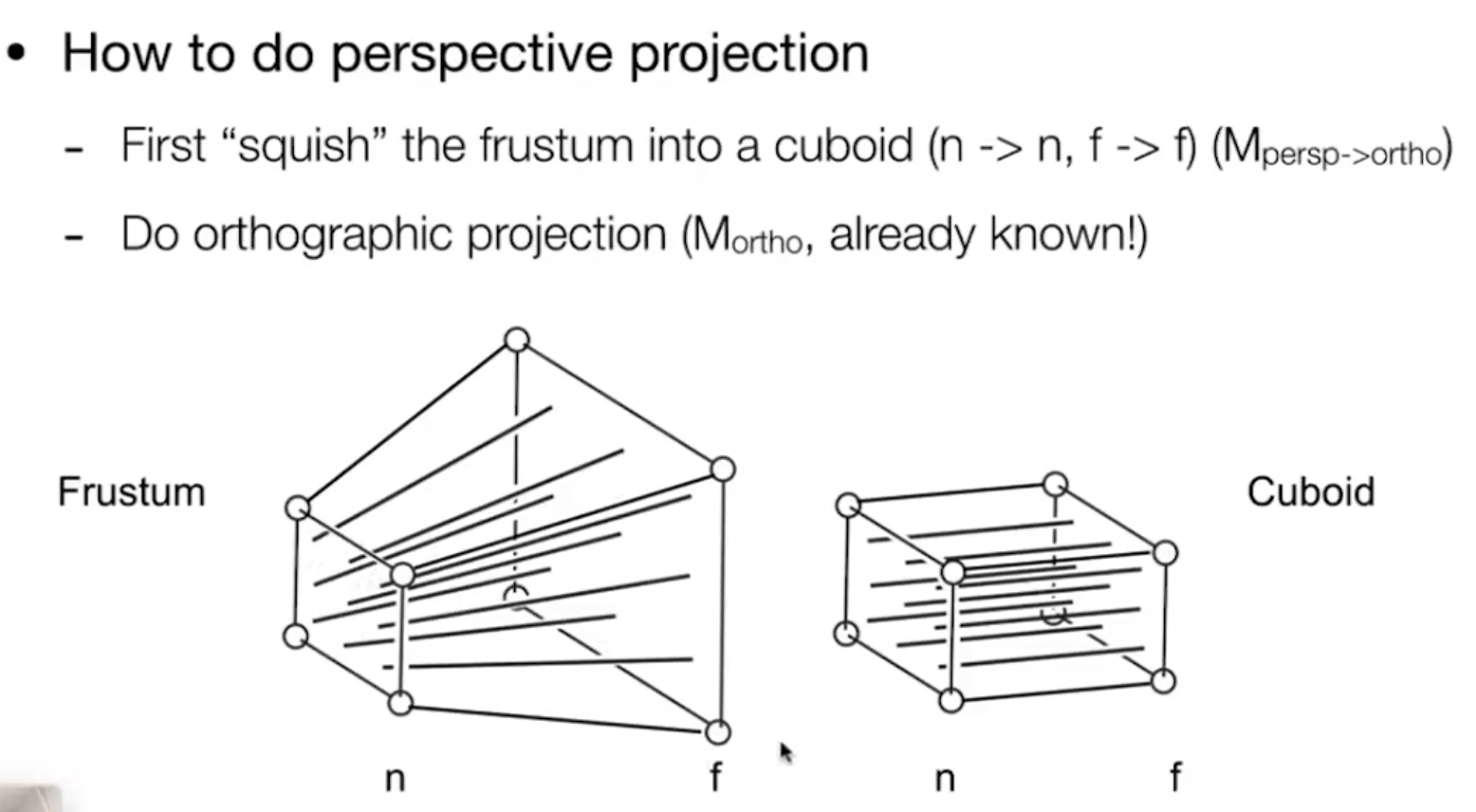
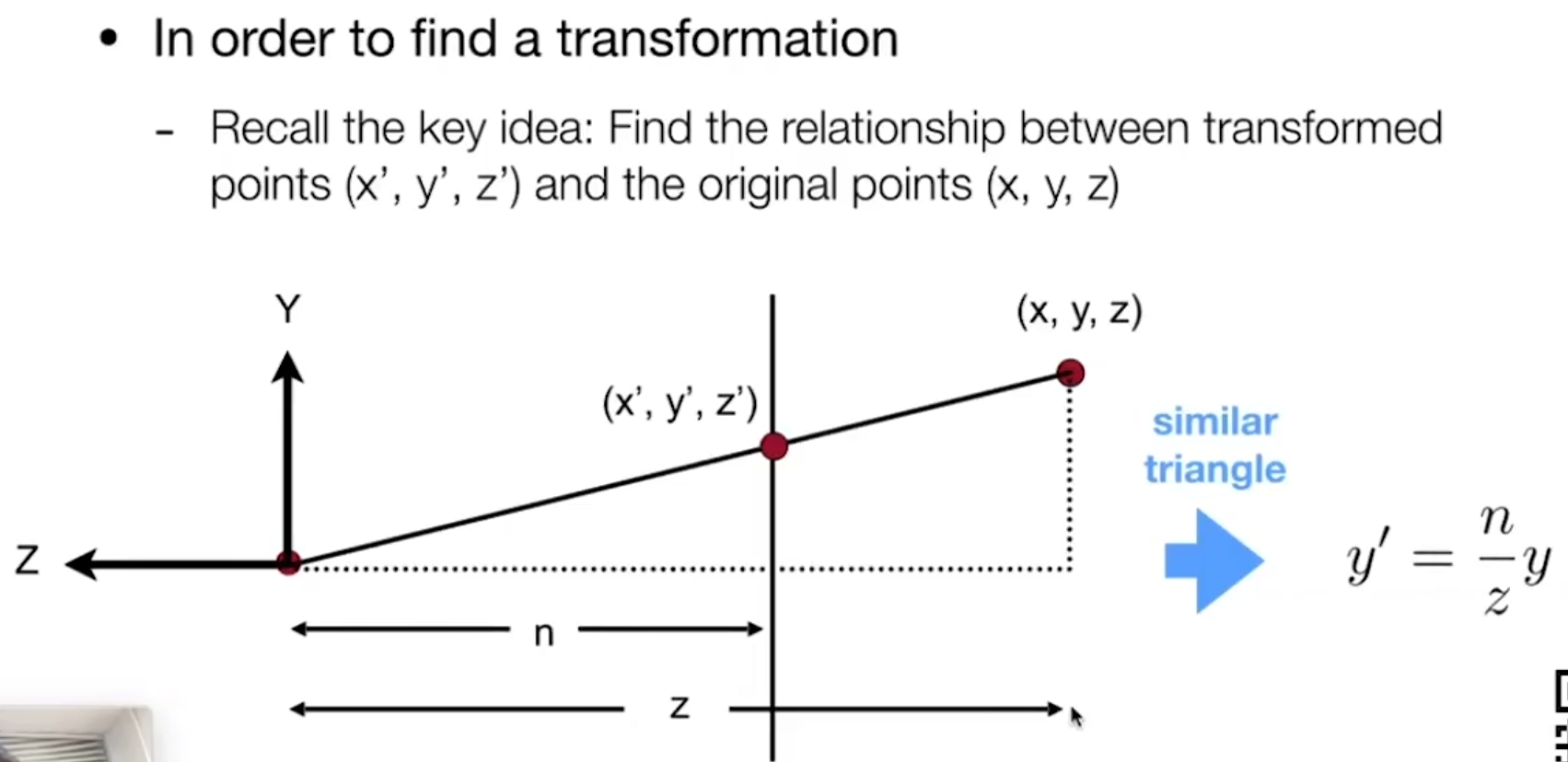
> 这里注意\(z\)是会变的！，参考射影变换的演示：

\[ M_{p \rightarrow o} = \begin{bmatrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0\\ 0 & 0 & n+f & -nf\\ 0 & 0 & 1 & 0 \end{bmatrix} \]

Lecture 05/06 Rasterization

需要一些傅里叶变换的前置知识

时域卷积=频域相乘，频域相乘=时域卷积 个人理解：走样是能从被采样（在频域被卷积以后的函数中恢复出原来的频率信息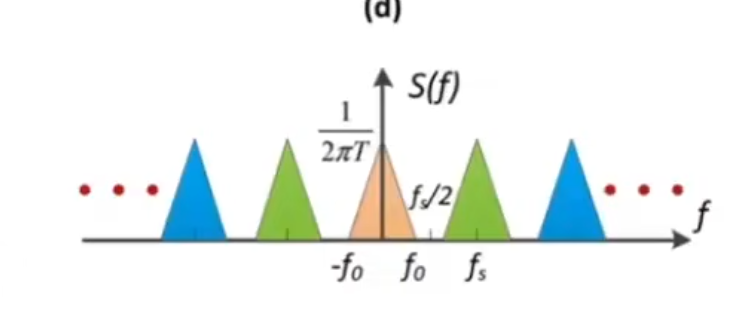）图中三角形重叠就是丢失了频率信息（从高频率开始）

Antialiasing 反走样

我把高频信号提前模糊了再去采样，牺牲高频信号保我的低频信号的准确性

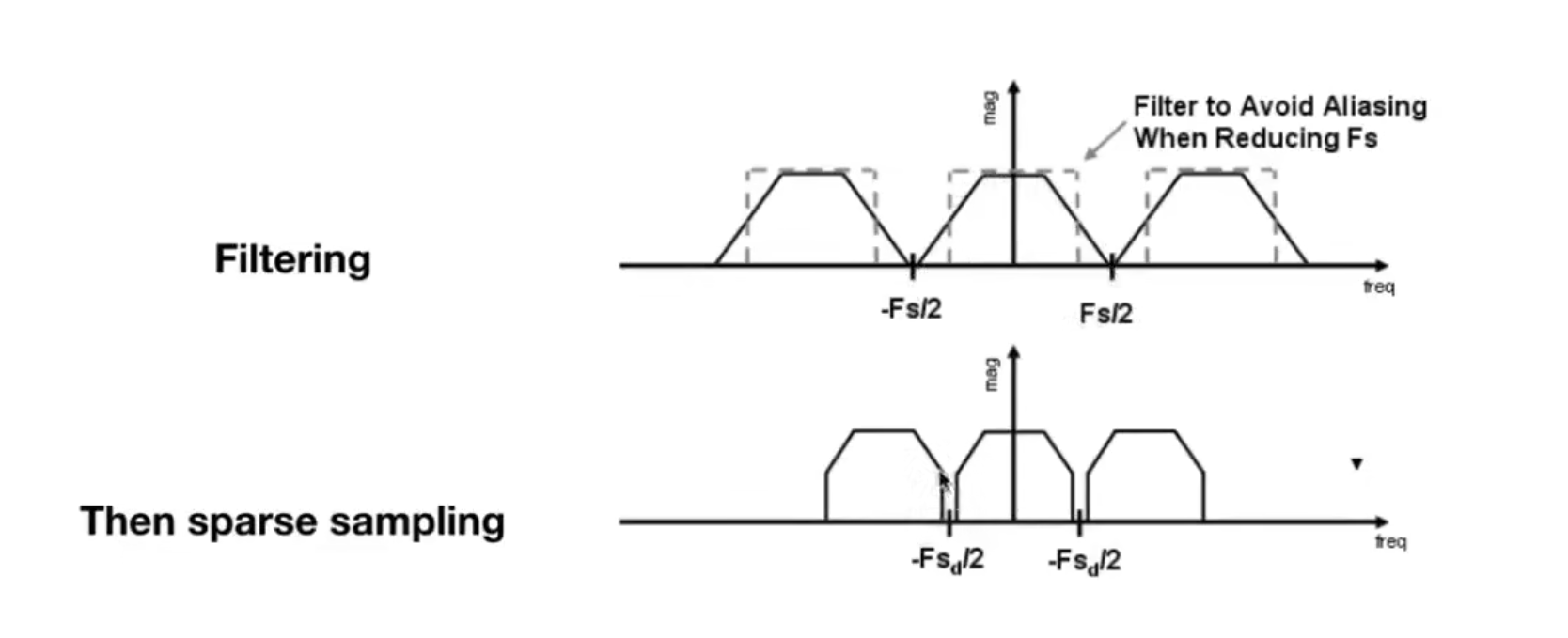
Multi-Sample Anti-Aliasing (MSAA)

一个格子多次取几个采样点（相当于做卷积低通滤波）

Fast Approximate AA (FXAA)

快速近似抗锯齿，是对采样后的图像单独处理边缘

Temporal AA (TAA)

可以简单理解为每一帧采样不同的点，做平均

Deep Learning Super Sampling (DLSS)

深度学习超分

Z-Buffering 深度缓存

简单遍历三角形维护最前的那个，复杂度\(O(N)\)

Lecture 06/07/08 Shading

Shading

Blinn-Phong 模型

Diffuse 漫反射

和观测方向\(v\)没有关系，到达的能量乘以和法线夹角的余弦

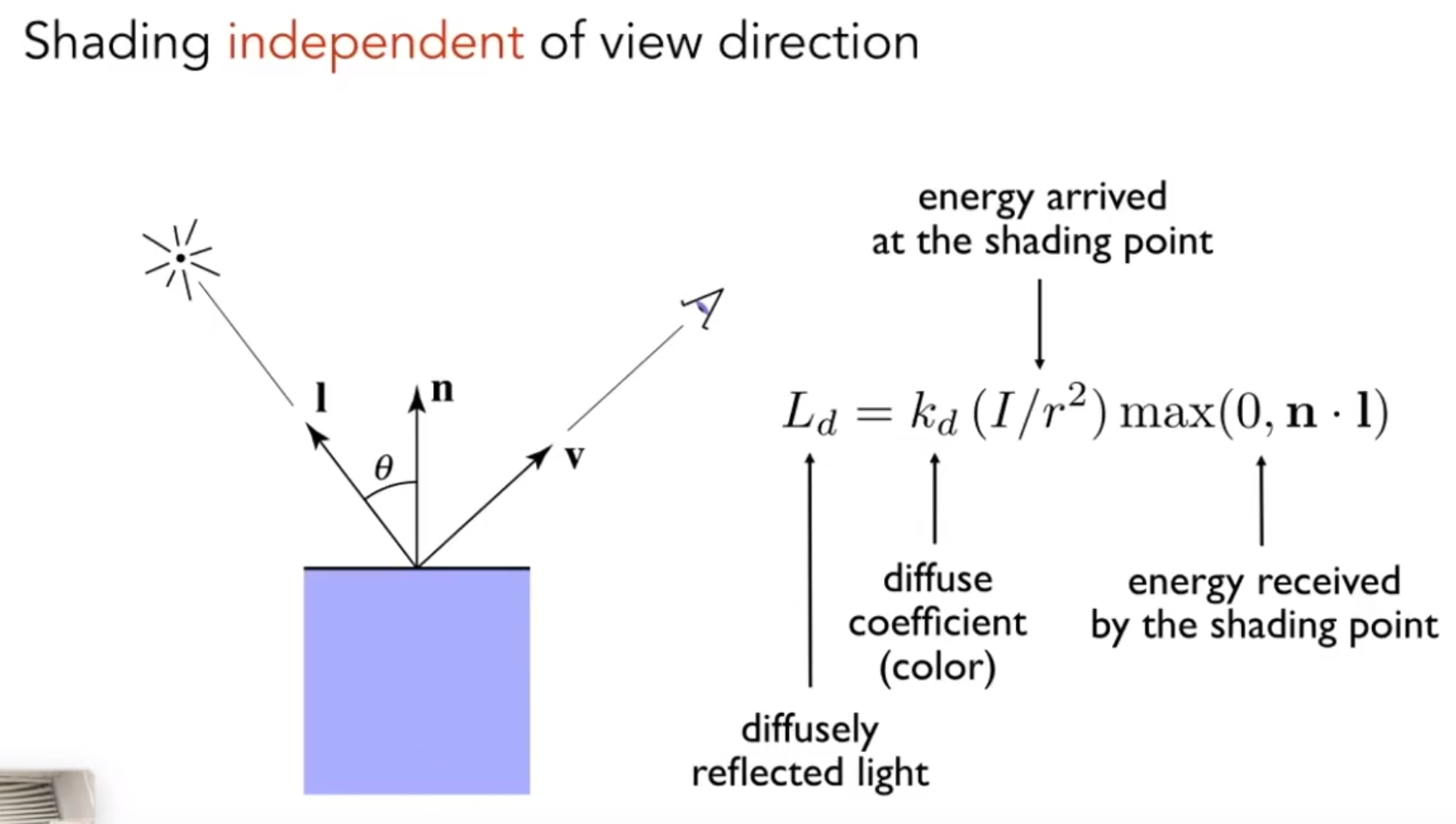
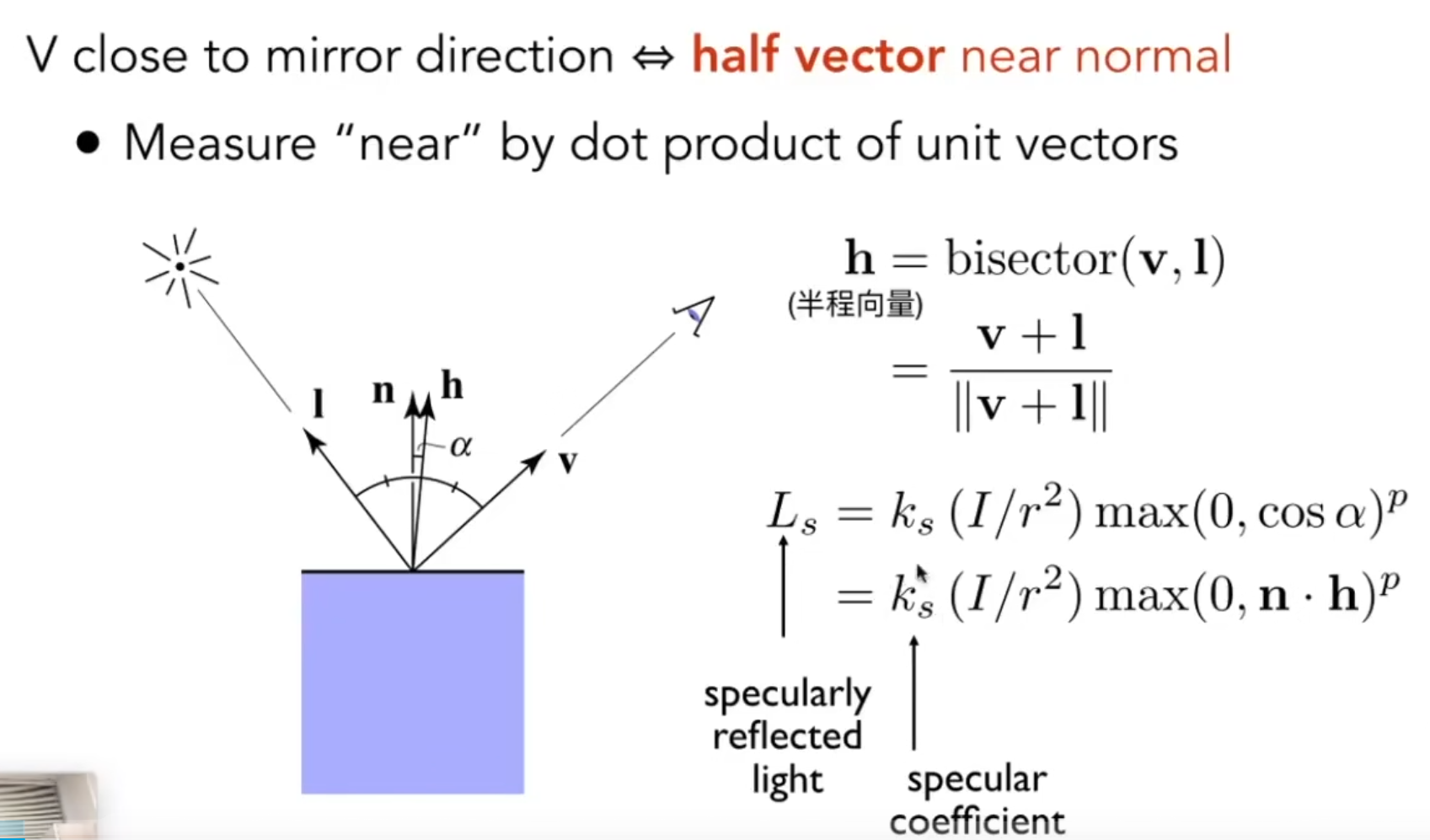
Specular 高光

Ambient 环境光

几种着色方式

Flat shading

逐三角形着色

Gouraud shading

逐顶点着色

Phong shading

逐像素着色

Pipeline 实时渲染管线

MVP变换在顶点变换阶段着色可能在顶点，可能在片元，控制他的代码就是shader

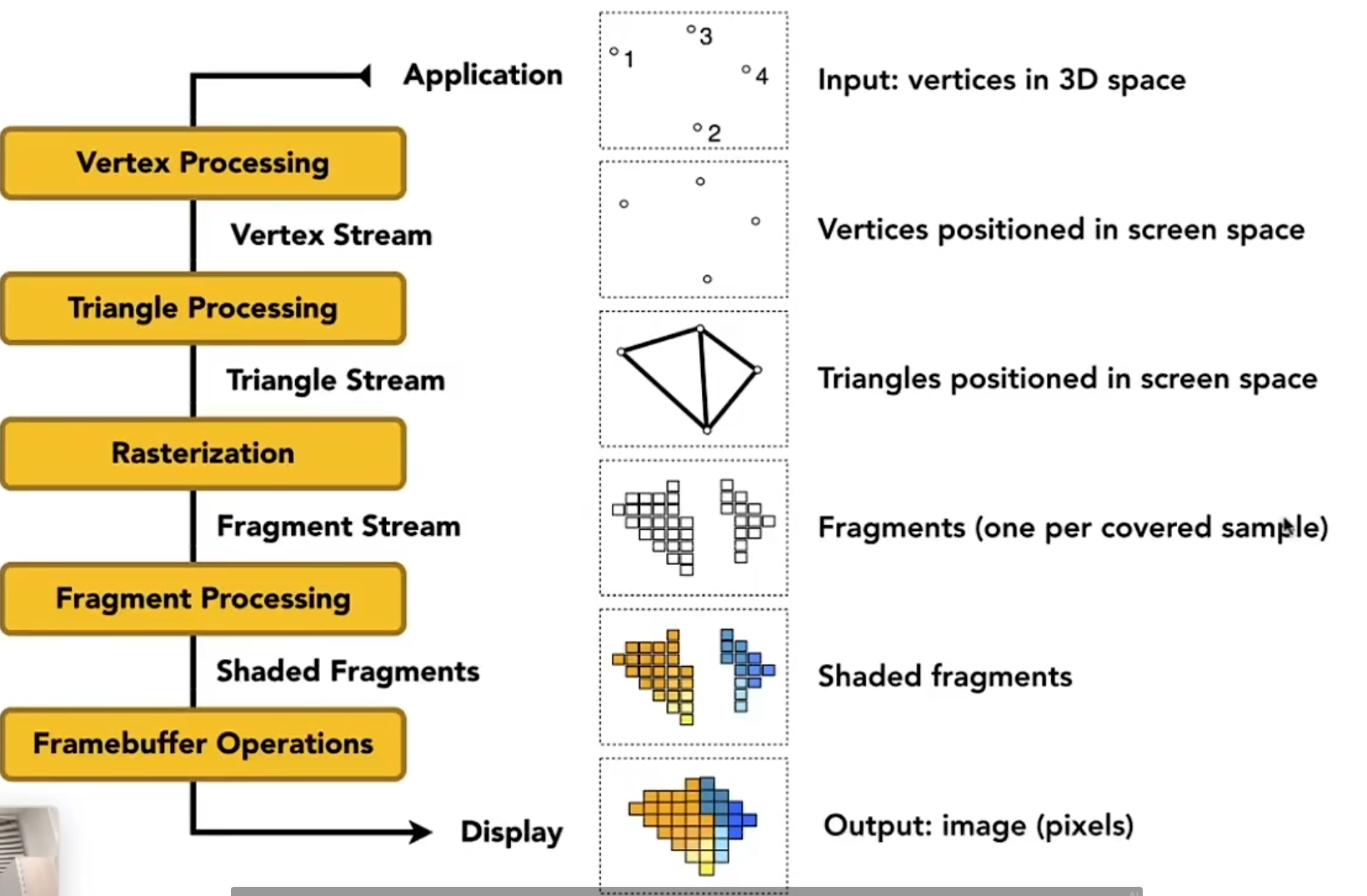
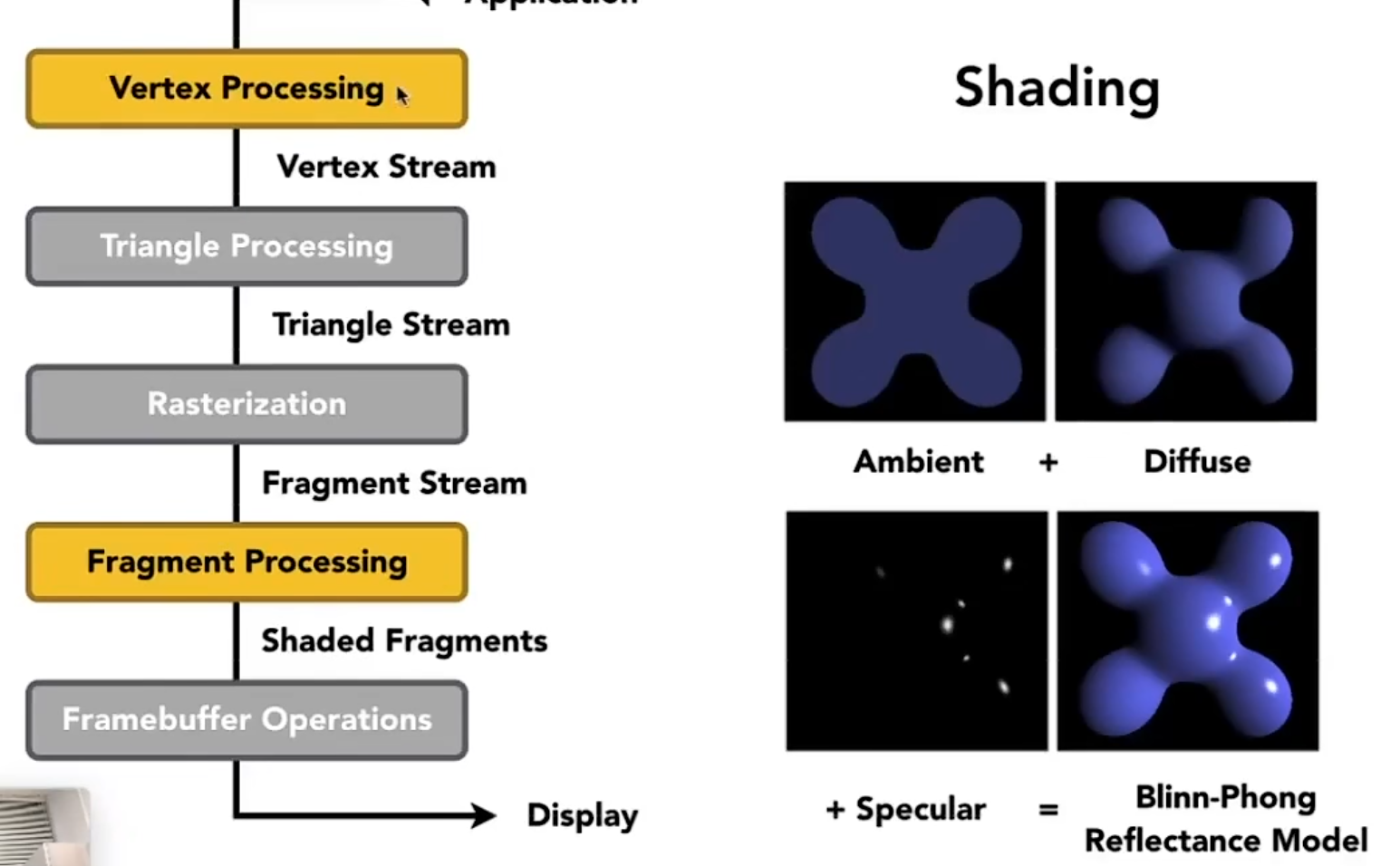
Texture Mapping

纹理=定义任何一个点的某种属性 坐标系=uv坐标系 Tiling 四方连续贴图

重心坐标

对着的三角形的面积/整个三角形的面积 得在投影变换前进行，投影变换近大远小会改变面积比（非仿射变换）

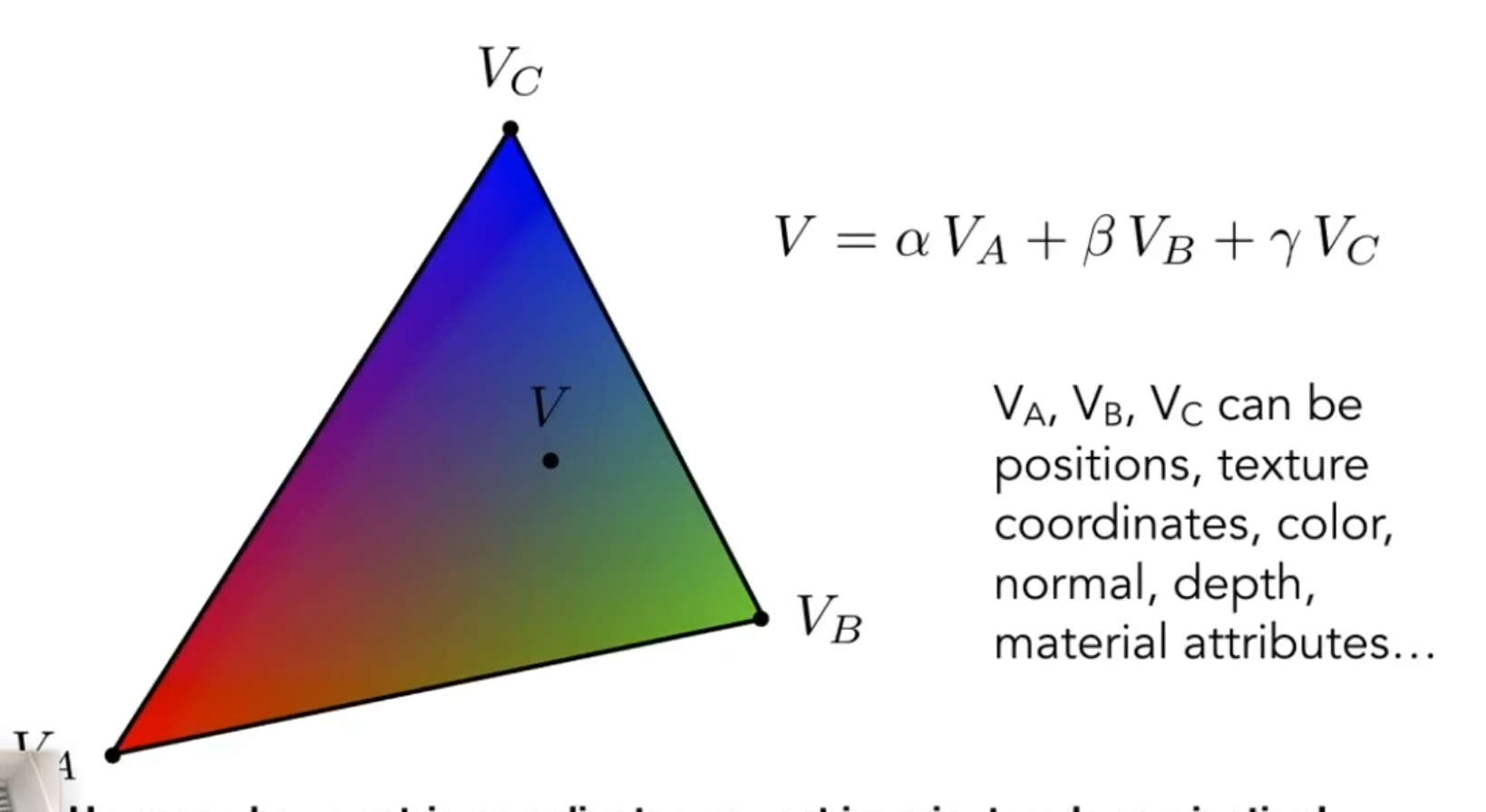
贴图采样

双线性插值 Bilinear

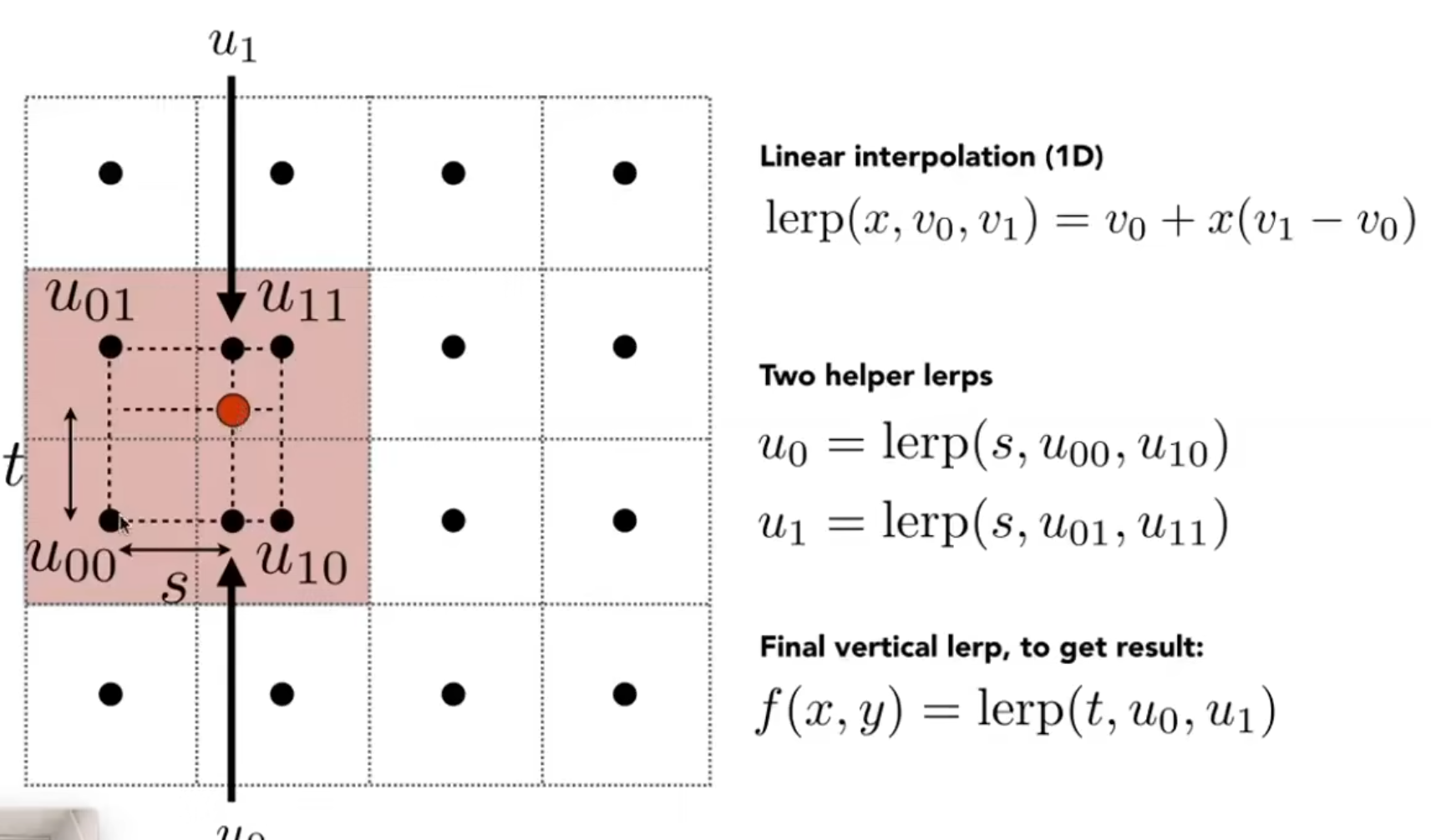
双三次插值 Bicubic

效果更好，复杂度更高

Mipmap

三分之一的额外空间开销

Mipmap Level

找刚好能让一个图素覆盖一个像素的那一层，为D

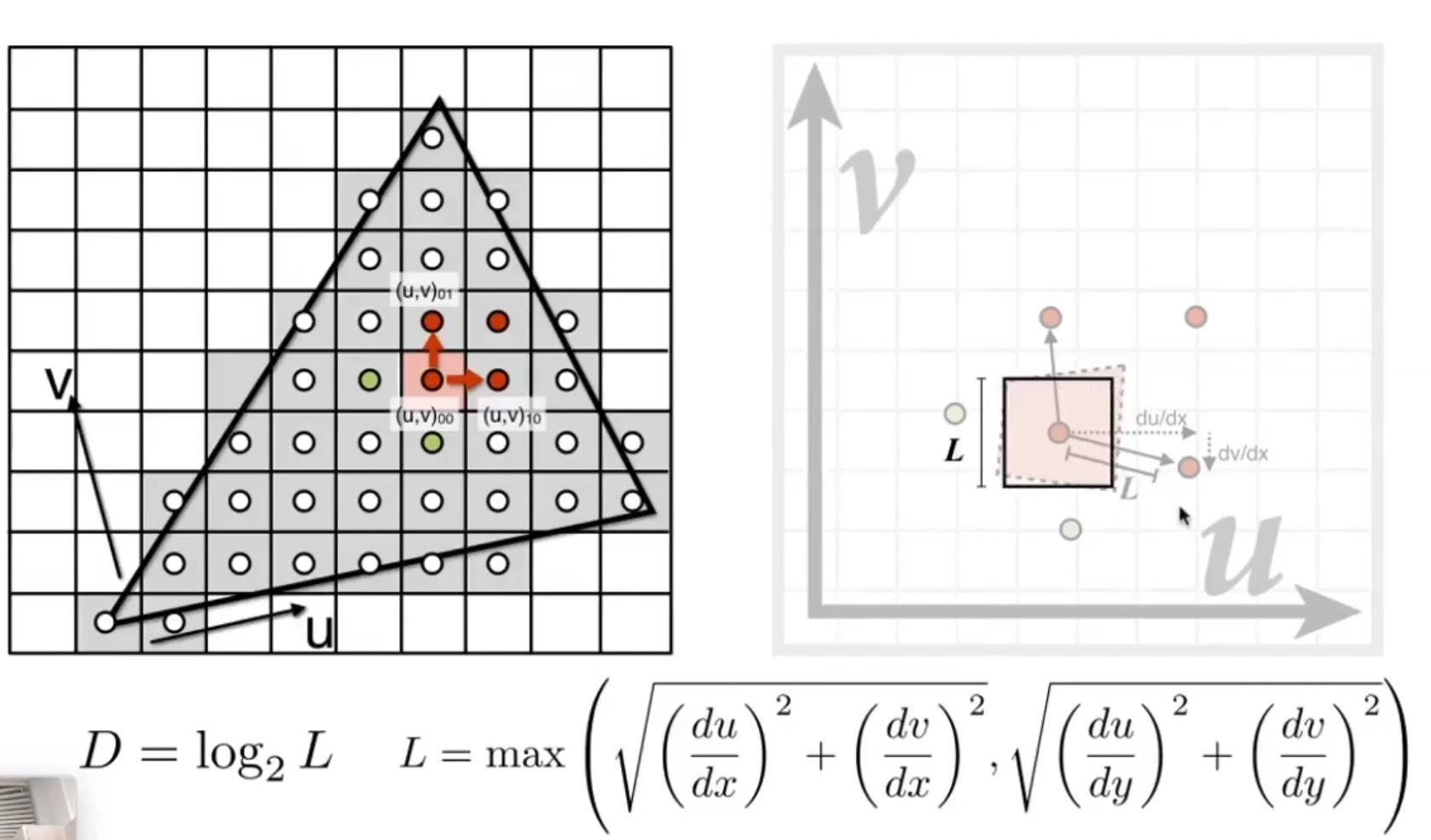
三线性插值

很简单粗暴的插值了三次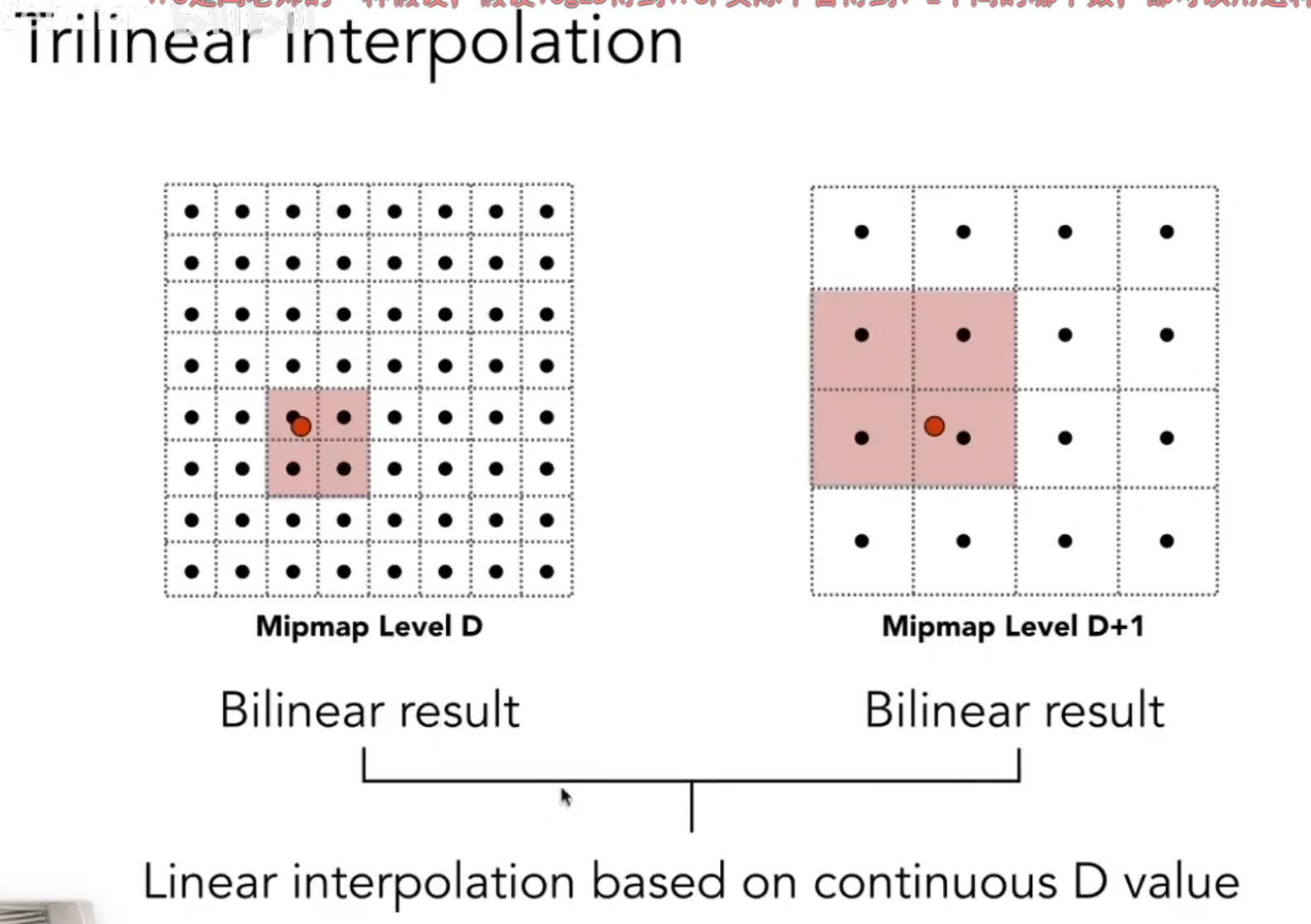

各向异性过滤

映射有时候会变成长条！三线性插值对这种长条效果并不好，怎么办呢我改一下mipmap的存储方法，来改善长条形状（长宽上的各项异性）的查询效果，多三倍空间开销（看实际情况），没什么多的计算开销，叫Ripmap但是斜着的还是不太对，有其他方法，比如圆形多次采样，有多的计算开销